Sus elementos notables son el radio y el centro.
La esfera es una figura geométrica de uso común, debido que es la figura utilizada para representar la Tierra, con lo cual, de manera continua se interactúa, ello obedece al deseo y la necesidad de estudiar las características y los aspectos geográficos de la Tierra.
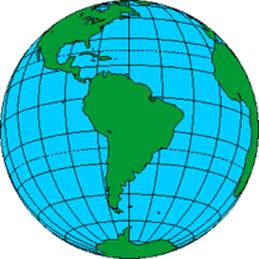
En la esfera terrestre, que es una representación esférica, tridimensional, un modelo reducido que imita a la Tierra. En ella están claramente definidos los paralelos y meridianos (que son líneas imaginarias que nos sirven para medir la longitud y la latitud de cualquier punto). Las dos más importantes son: la línea Equinoccial o Ecuador (Paralelo 0) y el Meridiano de Greenwinch (Meridiano 0).
PARTES DE LA ESFERA
HUSO ESFÉRICO
El huso esférico es la parte de la superficie de una esfera comprendida entre dos planos que se cortan en el diámetro de aquella.
ÁREA DEL USO ESFÉRICO:
CUÑA ESFÉRICA
La cuña esférica es la parte de una esfera comprendida entre dos planos que se cortan en el diámetro de aquella.
CASQUETE ESFÉRICO
Un casquete esférico, en geometría, es la parte de una esfera cortada por un plano. Si dicho plano pasa por el centro de la esfera, lógicamente, la altura del casquete es igual al radio de la esfera, y el casquete esférico será un hemisferio (semiesfera).
Si el radio de la esfera es , el radio de la base del casquete
, el radio de la base del casquete  , y la altura del casquete
, y la altura del casquete  , el área de la superficie curva del casquete esférico es:
, el área de la superficie curva del casquete esférico es:
el radio de la esfera se lo puede relacionar con el radio de la base del casquete y con la altura de este a través del teorema de Pitágoras:
reemplazando esto en la fórmula anterior del área se obtiene otra formula en función de y
y  .
.
PARTES DE LA ESFERA
HUSO ESFÉRICO
El huso esférico es la parte de la superficie de una esfera comprendida entre dos planos que se cortan en el diámetro de aquella.
ÁREA DEL USO ESFÉRICO:
CUÑA ESFÉRICA
La cuña esférica es la parte de una esfera comprendida entre dos planos que se cortan en el diámetro de aquella.
VOLUMEN DE LA CUÑA ESFÉRICA
CASQUETE ESFÉRICO
Un casquete esférico, en geometría, es la parte de una esfera cortada por un plano. Si dicho plano pasa por el centro de la esfera, lógicamente, la altura del casquete es igual al radio de la esfera, y el casquete esférico será un hemisferio (semiesfera).
Si el radio de la esfera es
 , el radio de la base del casquete
, el radio de la base del casquete  , y la altura del casquete
, y la altura del casquete  , el área de la superficie curva del casquete esférico es:
, el área de la superficie curva del casquete esférico es:el radio de la esfera se lo puede relacionar con el radio de la base del casquete y con la altura de este a través del teorema de Pitágoras:
reemplazando esto en la fórmula anterior del área se obtiene otra formula en función de
 y
y  .
.
Otra expresión para hallar el volumen del casquete esférico, en función del radio de la esfera y de la altura del casquete, es:
Haz clic en el siguiente enlace para observar las partes de la esfera.
http://recursostic.educacion.es/descartes/web/materiales_didacticos/construccion_esfericos/construccion_esfericos.htm
OBSERVA EL VÍDEO PARA COMPLEMENTAR TU APRENDIZAJE
PROBLEMA N° 01.
Calcular el área y el volumen de una esfera inscrita en un cilindro de 2 m de altura.
PROBLEMA N° 02.
PROBLEMA N° 03
Una mesa tiene un agujero circular con un diámetro de 12 cm. Sobre el agujero hay una esfera de diámetro 20 cm. Si la mesa tiene 30 cm de altura, ¿cuál es la distancia en centímetros desde el punto más alto de la esfera hasta el piso?
| (a) 40 cm | (b) 42 cm | (c) 45 cm | (d) 48 cm | (e) 50 cm |
PROBLEMA N° 04
En el rectángulo de la figura está inscrita una semicircunferencia. Si el largo del rectángulo mide 12 cm, ¿cuál es el volumen del cuerpo que se genera al hacer girar indefinidamente la figura sombreada en torno al lado
| (a) 142π cm3 | (b) 143π cm3 | (c) 144π cm3 | (d) 145π cm3 | (e) 146π cm3 |
HAZLO TÚ
MÁS PROBLEMAS
1) Calcula la superficie esférica y el volumen de una esfera de radio menor, si el área de otra mayor es 144π cm2 y la razón entre los volúmenes de las dos esferas es 3/4. (Rpta: 373,06 cm2)
2) El volumen de una esfera es de 32 cm3. Calcula el área de la sección transversal que pasa por su diámetro. (Rpta: 12,19 cm2)
3) La sección transversal que pasa por el diámetro de una esfera mide 62,8 cm2. Calcula el volumen de la esfera. (Rpta: 374,47 32 cm3)
4) El área de una superficie esférica es 196π cm2. Calcula el volumen de otra esfera cuyo radio mide el triple que la esfera anterior. (Rpta: 38 772,72 cm3)
5) La diferencia entre las superficies de dos esferas es 18,1 m2 y sus radios son proporcionales a 5 y 3. Calcula sus radios. (Rpta: R1 =1,5 y R2=0,9)
6) La cúpula semiesférica de una iglesia tiene 12 m de diámetro. ¿Cuánto costará pintarla sabiendo que se paga a razón de S/. 48 el metro cuadrado? (Rpta: S/. 10 851,84)
7) Una esfera de radio 6 cm tiene el mismo volumen que un cono de radio 6 cm. Calcula la altura del cono. (Rpta: 24 cm)
8) Halla el área de una superficie esférica cuya circunferencia máxima mide 140 m. (Rpta: 6 240, 36 m2)
9) El área de una superficie esférica es 256 m2. Halla el área del círculo máximo de la esfera. (Rpta: 64 m2)
10) Calcula el radio de una esfera cuya superficie es igual a la de un cilidro de 100 cm2. (Rpta: 2,82 cm)












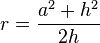










me ayudo esta informacion acerca de las esferas....................graxias
ResponderEliminar